Simple Transformations of 2-Dimensional Shapes
See also: Properties of PolygonsPlane shapes in two dimensions (drawn on a flat piece of paper for example) have measurable properties apart from just their physical measurements of side lengths, internal angles and area. They can undergo transformations, whereby they can change position or size, or ‘aspect ratio’ (how tall and thin or short and wide they are).
This page explores congruence, symmetry, reflection, translation and rotation. These concepts are about how a shape’s position changes, relative to a reference, such as a line or a point.
We are faced with these ideas regularly in everyday life, in everything from product design, architecture and engineering, to occurrences in the natural world. Even matching the pattern on a roll of wallpaper involves these geometric ideas.
Congruence
Mathematics is full of complex terminology, but sometimes a complicated term can mean something really simple. This is true for congruence.
Two shapes that are congruent have the same size and the same shape. It’s as simple as that!
In the diagram below, shapes A, B, C and D are all congruent. Shapes E, F, G and H are not congruent.
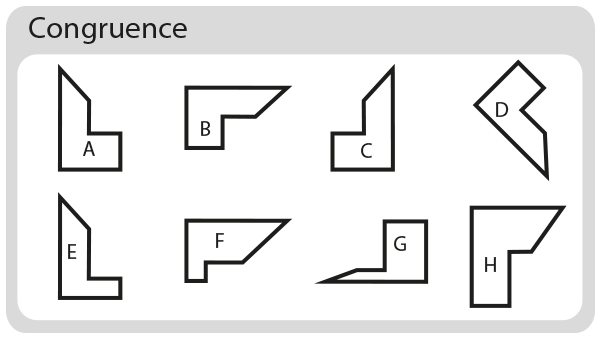
Shapes can be congruent even if they have been rotated or reflected.
Take a piece of tracing paper and trace over shape A. The traced shape can be placed exactly over shape B. You have to rotate it through 90°, but it is still the same.
To fit your traced shape A over Shape C, you need to turn the tracing paper over. This is a reflection of shape A, but it is still the same.
Then if you rotate it some more, you reach shape D.
Now take your traced shape A and try to fit it exactly over shapes E, F G and H. It doesn’t matter how many times you rotate or turn over your paper, it will not fit exactly. These shapes therefore cannot be described as congruent with shapes A, B, C and D.
Congruence is Comparative
Shape A cannot be described as ‘congruent’ on its own. If you look at Shape A on its own, you can say that it is an irregular hexagon and you can measure its perimeter and area. However, it cannot be described as congruent until there is another shape to compare it to.
Shape G for example is not congruent with any of the other shapes in our diagram. But if you have a group of shapes all the same as shape G, then shape G would be congruent with all of those shapes.
Symmetry
A shape can be described as symmetrical if it has a property that mathematicians refer to as symmetry.
The simplest form of symmetry is line symmetry.
Line symmetry is a form of reflection (which is covered later in this page) and is sometimes referred to as mirror symmetry. This means that if you were to place a mirror along the line of symmetry, then the reflection of the shape in the mirror would be identical to the shape without the mirror in place.
The letter A, for example, has a single vertical line of symmetry, from the apex to the base:
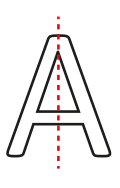
It is possible for shapes to have multiple lines of symmetry. In fact, for regular polygons, the number of lines of symmetry is the same as the number of sides of the shape. So a hexagon (six sides) has six lines of symmetry and a dodecagon (12 sides) has 12 lines of symmetry. A circle therefore has an infinite number of lines of symmetry.
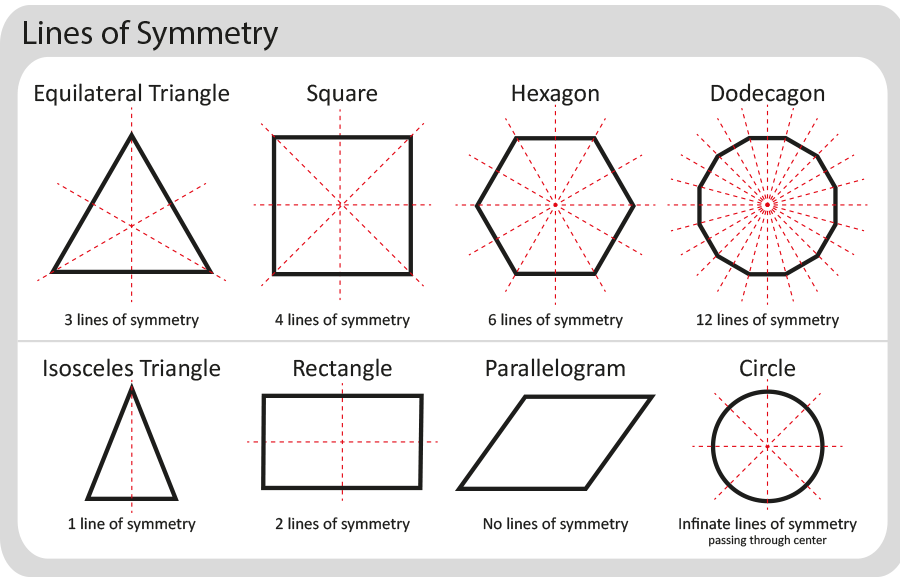
Asymmetry
If a shape does not have any lines of symmetry, such as the shape in the congruence example, it is described as asymmetric. This is also true of the trapezoid and parallelogram shown in the diagram above.
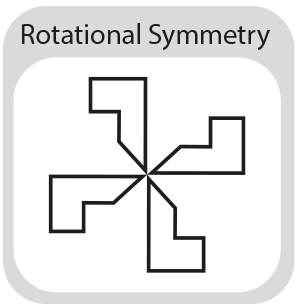
Another common form of symmetry is rotational symmetry. If you rotate something, you simply turn it. This is the same with rotational symmetry - the shape is rotated an exact number of times about a point.
The order of rotational symmetry is the number of times the shape is replicated in one full rotation. The repeats are always at regular angles, like the sides on a regular polygon.

The most commonly recognised example of rotational symmetry is possibly the recycling symbol with three arrows.
This familiar logo has a rotational symmetry of order 3, i.e. the shape is replicated three times when rotated about the centre point of the logo.
Any shape can have rotational symmetry – the diagram below shows shape A from our congruence example, with an order of 4:
Reflection
In the section on mirror symmetry above, we learned that if a mirror is placed along the line of symmetry, then the reflected image looks the same as the image without the mirror. This is a specific type of reflection. A mirror line or line of reflection can exist anywhere relative to a shape, not just along a line of symmetry. The image of the shape on the other side of the mirror line is its reflection.
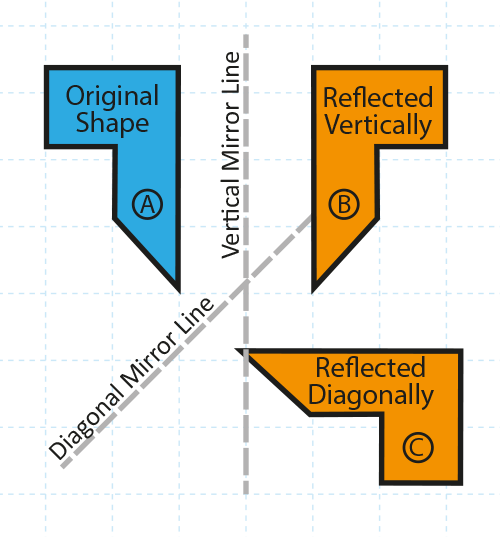
In the diagram below, A is the original shape. The simplest reflection to understand is when shape A is reflected in a vertical mirror line that is parallel to its longest side. The reflected shape is B.
A mirror line can be placed anywhere and at any angle to the original shape. The diagonal mirror line is at approximately 45° to the longest side of shape A and the reflected shape is C.
Drawing reflected shapes
When you need to draw the reflection of a shape on a page, you can get an idea of what it will look like using a mirror.
You can trace your image onto tracing paper, then fold the paper along the line of reflection (or mirror line) and then trace the reflection. But if you need to draw it accurately, you will need some graph paper and a logical approach.
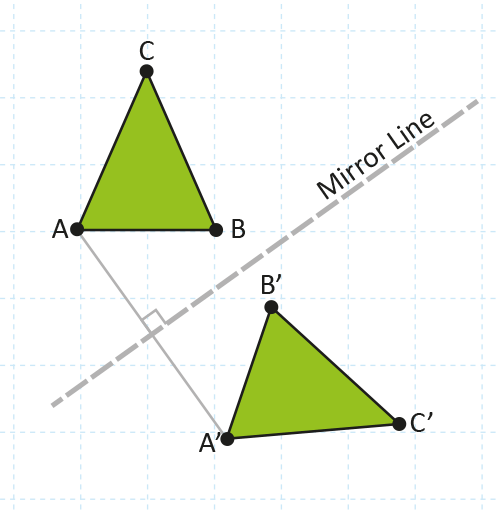
In the diagram above, the original triangle is labelled ABC. The mirror line is drawn in red and is labelled line of reflection.
Triangle ABC reflected in the mirror line is triangle A’B’C’.
The Rules of Reflection
-
Each point and its reflection are exactly the same distance from the mirror line.
The line that connects a point with its reflection is perpendicular (at right angles) to the mirror line.
In the diagram, the line connecting point A to A’ is called a construction line and illustrates these rules: The distance between A and the mirror line is the same as the distance between A’ and the mirror line; and the construction line is perpendicular to the mirror line (shown by the small square at its centre).
When you are drawing a reflected shape, you need to use this systematic approach:
Start at one corner (point A in our example) and draw a construction line from that point across the mirror line. Use a protractor or a set square to make sure this line is at right angles to the mirror line.
Accurately measure the distance along the construction line from the point (A) to the mirror line and make a note of the measurement. Starting at the point where the construction line and mirror line intersect (cross), now measure the same distance along the construction line on the opposite side of the mirror line and draw a dot at this point. This is your point A’.
Repeat the process for points B and C (or more, depending on your shape), then carefully join your reflected points in the order than you drew them, to create your reflected shape.
This all sounds very tricky but it becomes easier with practise. It can be a fun exercise to hone your spatial skills.
Translation
Translation is another of those maths terms that sounds much more difficult than it is. In fact it is really easy!
Translation is the movement of a shape from one place to another without rotation or reflection.
That is to say, if every point on the original shape moves along a straight line, exactly the same distance and in exactly the same direction (at the same angle), then this is a translation of that shape.
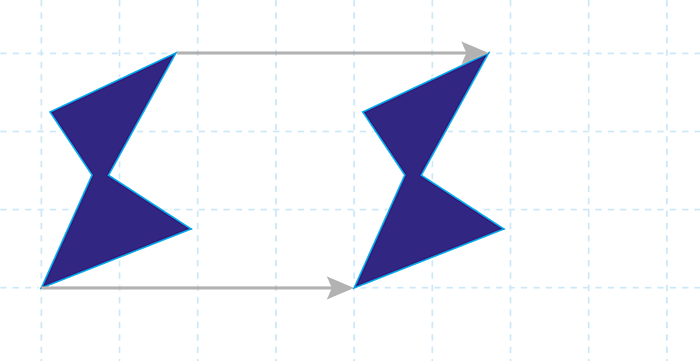
The diagram above illustrates translation – each point in the shape on the left is moved four squares to the right.
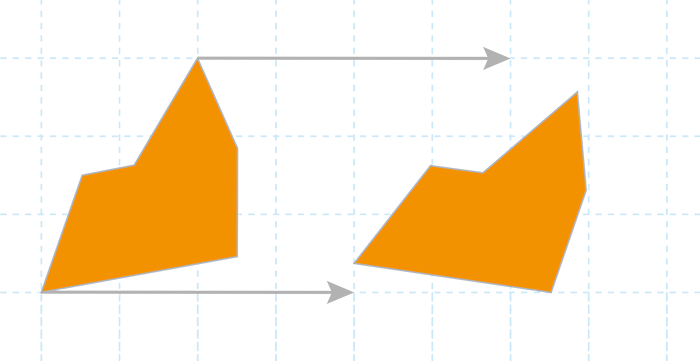
However, the diagram below cannot be described as a translation, because the shape is both translated (moved in a straight line) and rotated:
A note on Vectors
In the diagram below, each point on the original shape is translated five squares to the right and two squares vertically down:
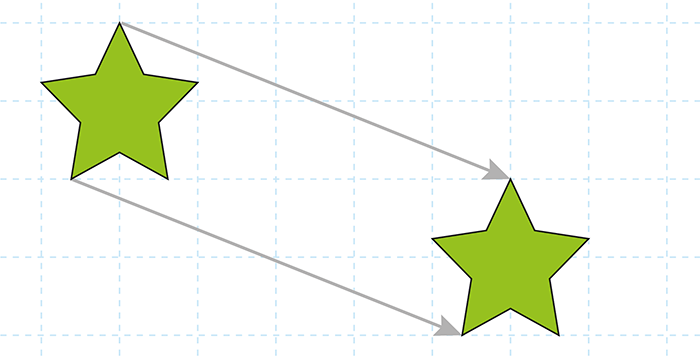
A mathematical tool called a column vector can be used to describe this translation. This is two numbers in brackets aligned vertically (in a column).
So \(\begin{bmatrix} 5 \\ -2 \end{bmatrix}\) is the translation 5 units to the right and 2 units downwards.
Vectors are presented in the form \(\begin{bmatrix} x \\ y \end{bmatrix}\)
Where \(x\) is the horizontal axis (positive translations to the right, negative to the left) and \(y\) is the vertical axis (positive upwards, negative downwards, hence why the translation of two units downwards is written −2).
For more on \(x\) and \(y\) axes, see our page on Cartesian coordinates.
Vectors are incredibly useful in mathematics, because they are able to describe things that have both magnitude and direction. Vectors are very important in many applications and the study of motion is an example. In this case, vector quantities include velocity, acceleration, force, displacement and momentum.
Rotation
We discovered the concept of rotation of a shape in the section of rotational symmetry above. In the case of rotational symmetry, the shape was rotated and repeated at precise angular intervals about its centre.
Rotation of a shape without symmetry can be through any angle, clockwise or anticlockwise, about a single point. This point is important, and it is called the centre of rotation.
The diagram below shows a right-angled triangle A rotated about a point O. Triangle B is what it looks like when it is rotated anticlockwise through 90°. Triangle C is triangle A rotated clockwise through 180°.
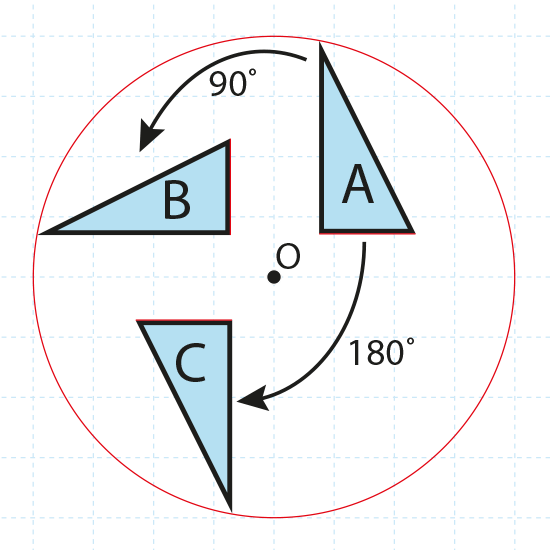
The rule of rotation:
The distance of any point on the shape from the centre of rotation always stays the same.
So if you were to take a compass, place its point at the centre of rotation, and join the apex of each of the triangles in the diagram above, then you would have drawn a perfect circle - as indicated by the red circle.
Further Reading from Skills You Need
Understanding Geometry
Part of The Skills You Need Guide to Numeracy
This eBook covers the basics of geometry and looks at the properties of shapes, lines and solids. These concepts are built up through the book, with worked examples and opportunities for you to practise your new skills.
Whether you want to brush up on your basics, or help your children with their learning, this is the book for you.
Conclusion
Two dimensional shapes are rarely found in isolation in the real world, but are repeated, reflected, translated and rotated. These are what mathematicians call transformations. We find examples in everything from product logos to huge engineering structures and architectural masterpieces.
There are many more mathematically complex types of transformation, for which more advanced concepts such as vectors become useful. While this page only gives an introduction to some of the basic concepts, it has hopefully left you with plenty to REFLECT on!
Continue to:
Calculating Area
Angles

