Our page on Cartesian Coordinates introduces the simplest type of coordinate system, where the reference axes are orthogonal (at right angles) to each other. In most everyday applications, such as drawing a graph or reading a map, you would use the principles of Cartesian coordinate systems. In these situations, the exact, unique position of each data point or map reference is defined by a pair of (x,y) coordinates (or (x,y,z) in three dimensions). The coordinates are the point’s ‘address’, its location relative to a known position called the origin, within a two- or three-dimensional grid on a flat surface or rectangular 3D space.

However, some applications involve curved lines, surfaces and spaces. Here, Cartesian coordinates are difficult to use and it becomes necessary to use a system derived from circular shapes, such as polar, spherical or cylindrical coordinate systems.

---

Why are Polar, Spherical and Cylindrical Coordinates Important?

In everyday situations, it is much more likely that you will encounter Cartesian coordinate systems than polar, spherical or cylindrical. However, two-dimensional polar coordinates and their three-dimensional relatives are used in a wide range of applications from engineering and aviation, to computer animation and architecture.

You may need to use polar coordinates in any context where there is circular, spherical or cylindrical symmetry in the form of a physical object, or some kind of circular or orbital (oscillatory) motion.

What does that mean?

Physically curved forms or structures include discs, cylinders, globes or domes. These could be anything from pressure vessels containing liquified gases to the many examples of dome structures in ancient and modern architectural masterpieces.

Physicists and engineers use polar coordinates when they are working with a curved trajectory of a moving object (dynamics), and when that movement is repeated back and forth (oscillation) or round and round (rotation). Examples include orbital motion, such as that of the planets and satellites, a swinging pendulum or mechanical vibration. In an electrical context, polar coordinates are used in the design of applications using alternating current; audio technicians use them to describe the ‘pick-up area’ of microphones; and they are used in the analysis of temperature and magnetic fields.

---

---

How are Polar, Spherical and Cylindrical Coordinates Defined?

In these cases and many more, it is more appropriate to use a measurement of distance along a line oriented in a radial direction (with its origin at the centre of the circle, sphere or arc) combined with an angle of rotation, than it is to use an orthogonal (Cartesian) coordinate system.

Trigonometry can then be used to convert between the two types of coordinate system. For more about this and the theory behind it, have a look at our pages on curved shapes, three-dimensional shapes and trigonometry.

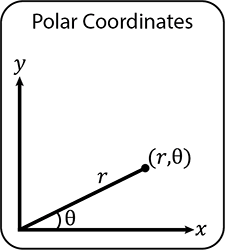
Polar Coordinates

In mathematical applications where it is necessary to use polar coordinates, any point on the plane is determined by its radial distance \(r\) from the origin (the centre of curvature, or a known position) and an angle theta \(\theta\) (measured in radians).

The angle \(\theta\) is always measured from the \(x\)-axis to the radial line from the origin to the point (see diagram).

In the same way that a point in Cartesian coordinates is defined by a pair of coordinates (\(x,y\)), in radial coordinates it is defined by the pair (\(r, \theta\)). Using Pythagoras and trigonometry, we can convert between Cartesian and polar coordinates:

$$r^2=x^2+y^2 \quad \text{and} \quad \tan\theta=\frac{y}{x}$$

And back again:

$$x=r\cos\theta \quad \text{and} \quad y=r\sin\theta$$

Spherical and Cylindrical Coordinate Systems

These systems are the three-dimensional relatives of the two-dimensional polar coordinate system.

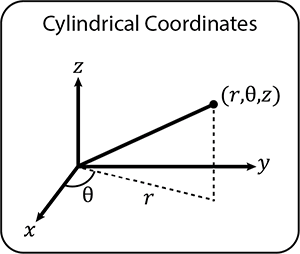
Cylindrical coordinates are more straightforward to understand than spherical and are similar to the three dimensional Cartesian system (x,y,z). In this case, the orthogonal x-y plane is replaced by the polar plane and the vertical z-axis remains the same (see diagram).

The conversion between cylindrical and Cartesian systems is the same as for the polar system, with the addition of the z coordinate, which is the same for both:

$$r^2=x^2+y^2,\quad \tan\theta=\frac{y}{x}\quad \text{and} \quad z=z$$

$$x=r\cos\theta,\quad y=r\sin\theta\quad \text{and} \quad z=z$$

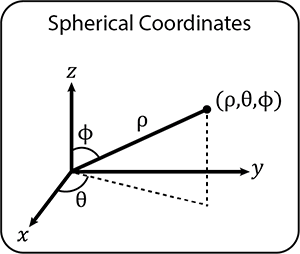
The spherical coordinate system is more complex. It is very unlikely that you will encounter it in day-to-day situations. It is primarily used in complex science and engineering applications. For example, electrical and gravitational fields show spherical symmetry.

Spherical coordinates define the position of a point by three coordinates rho (\(\rho\)), theta (\(\theta\)) and phi (\(\phi\)).

\(\rho\) is the distance from the origin (similar to \(r\) in polar coordinates), \(\theta\) is the same as the angle in polar coordinates and \(\phi\) is the angle between the \(z\)-axis and the line from the origin to the point.

In the same way as converting between Cartesian and polar or cylindrical coordinates, it is possible to convert between Cartesian and spherical coordinates:

$$x = \rho\sin\phi\cos\theta,\quad y=\rho\sin\phi\sin\theta\quad\text{and}\quad z=\rho\cos\phi$$

$$p^2=x^2+y^2+z^2,\quad\tan\theta =\frac{y}{x}\quad\text{and}\quad\tan\phi=\frac{\sqrt{x^2+y^2}}{z}$$

---

Latitude and Longitude, Maps and Navigation

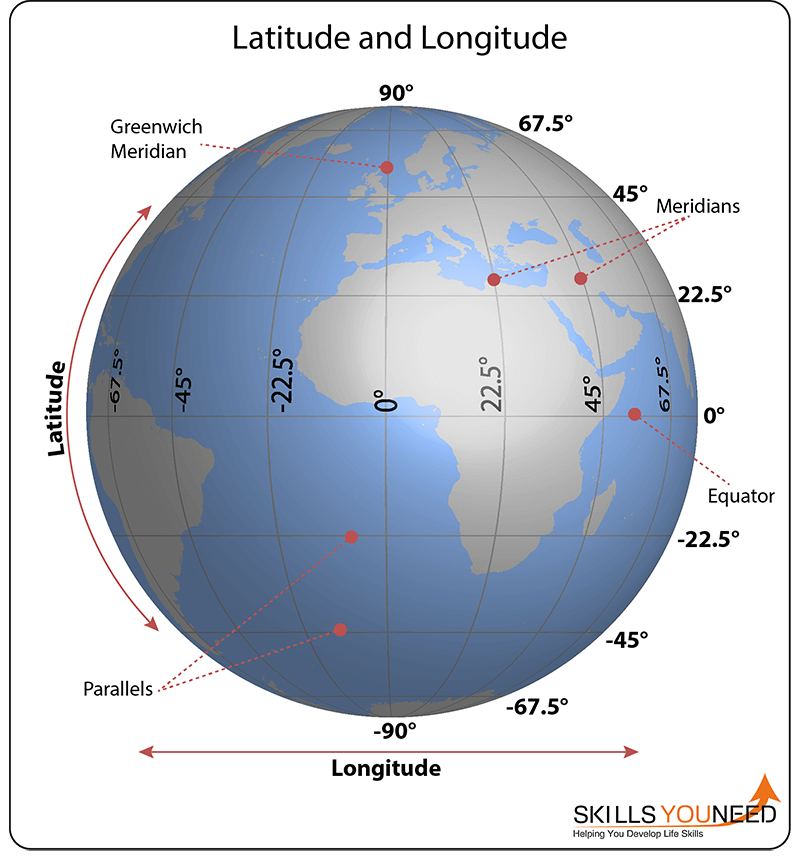
The most familiar application of spherical coordinates is the system of latitude and longitude that divides the Earth’s surface into a grid for navigational purposes. The distances between lines on the grid are not measured in miles or kilometres, but in degrees and minutes.

Lines of latitude are horizontal slices through the globe. The slice at the Equator is at 0° latitude and the poles are at ±90°. These lines are called parallels.

Lines of longitude are like the wedges of an orange, measured radially from a vertical line of symmetry connecting the poles. These lines are called meridians. The reference line of 0° longitude is known as the Greenwich Meridian, which passes through the Royal Observatory in Greenwich, London.

To use this 3D system for navigation however, the curved grid needs to be transferred onto flat ‘charts’ (maps of coastlines and the ocean floor for seafarers) using a projection. In this way, charts can be used like conventional maps with an orthogonal grid system, and the rules of Cartesian coordinates can be applied.

First imagine wrapping a piece of paper around a globe, making a cylinder. The image on the chart is projected from the three-dimensional sphere onto the two-dimensional sheet of paper. This is a specific method used by cartographers called the Mercator Projection.

The grid lines on a nautical chart are still in degrees and minutes and distances are measured in nautical miles. One nautical mile is the same as one minute of latitude.

---

Conclusion

It is unlikely that you will need to use polar or spherical coordinates unless you work in a role that specifically requires it, but it is helpful to be aware of what they are and how they are used.

It is also fascinating to understand how a map of a 3D shape like the globe can be translated into flat charts that have enabled seafarers to travel the globe for hundreds of years.

---